The turning effect of forces is a very important topic in Physics and there are multiple topics in this chapter which you need to learn.
First of all, you should know that a force may cause an object to rotate (clockwise or anticlockwise) around its pivot (a central point or shaft where an object turns).
This is known as the turning effect of a force or the moment of the force.
The turning effect of a force is mainly dependent upon two factors which are:
- The magnitude of the force
- The perpendicular distance from the pivot to the line of action of the force
The moment of a force (torque):
The torque (moment of a force) is the product of the force and the perpendicular distance from the line of action of the force to the pivot (central point).
In terms of an equation, this can be summed up as:
moment of a force = force (F) x distance (d)
M = F x d
The SI unit for torque (moment of a force) is newton metre (N m) because the symbol for force is newton and the symbol of distance is metre.
Note: The distance taken from the pivot to the line of action of the force will always be perpendicular.
There are multiple applications of turning effect in our daily life and some of them are mentioned below.
Examples of turning effect:
- The force applied by a worker to a spanner to rotate a nut.
- A person pushing a swing and making it rotate around its pivot.
- A force applied to a door-knob (making it swing around its hinge).
- A driver turning a steering wheel by applying a force on its rim.
- A person removing a bottle's cork by pushing down the bottle opener's lever.
These are some of the daily life applications of turning effect of a force.
Principle of moments:
According to the principle of moments, when a body is in equilibrium (balanced state), the sum of the anticlockwise moment about a pivot is equal to the sum of the clockwise moment about the same pivot.
In other words, you can say that torque 1 is equal to the torque 2 and in terms of formula, it can be said:
anticlockwise moment = clockwise moment
F1 x d1 = F2 x d2
Note: When an object is at equilibrium, the resultant force on the object is zero and the resultant moment on the object is also zero.
To ace this concept, you need to practice some questions which are listed below.
Question 1:
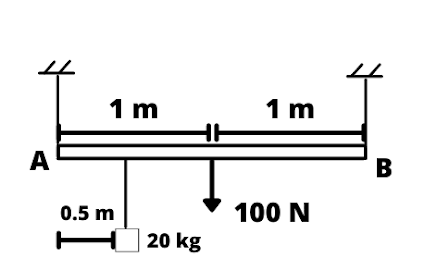
A uniform rod AB of length 2 m has a weight of 100 N carries a load of 20 kg as shown in the diagram below. It is supported by two strings at its end. Determine the tension in the strings.
Solution:
Let the tension of the string at A be T1
Let tension of the string at B be T2
The moment at A = F x d
100 x 1 + 200 x 0.5 = T2 x 2
T2 = 100 N
By applying the principle of the moment:
Sum of upward forces = sum of downward forces
T1 + T2 = 200 + 100 = 300 N (total force)
T1 = 300 - 100 = 200 N
Question 2:
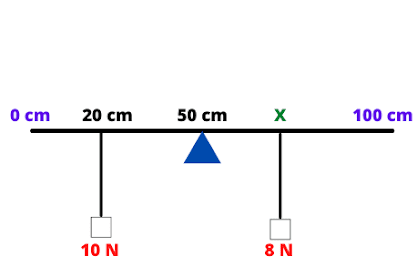
A uniform rule is balanced about a pivot at its midpoint when a 10 N weight is suspended from the 20 cm mark. One more weight of 8 N is suspended from another position (X).
Find the torque (moment) of the 10 N weight about the pivot and the position (X) from where the 8 N weight is suspended.
Solution:
We will solve this question in two parts. Firstly, we will calculate the moment around the 10 N force.
moment = F x d
moment = 10 x 0.30 (because 30 cm is 0.30 m)
moment = 3 N m
To find the unknown distance, we will apply the principle of the moment.
Let the unknown distance be d1;
clockwise moment = anticlockwise moment
8 x d1 = 10 x 0.30
d1 = 0.375 m
Position X = 0.50 - unknown distance = 0.50 - 0.375
Posiotion X = 0.875 m
Centre of gravity:
The centre of gravity (CG) of an object is when all sides are in balance and is the point at which the weight is equally dispersed.
Further reading:
In simple words, this is the point through which the weight of the whole body appears to act.
The objects which have a uniform density and regular shape (such as triangles, circles, cuboids, rectangles and spheres) have their centre of gravity at their geometric centre.
However, the centre of gravity of an irregular object is not its centre.
You can calculate it by following the procedure mentioned below:
- Draw a line on the object along the string.
- Use another point on the object to draw one more line.
- Now, you will have two lines that will intersect (cut) each other.
- The point of intersection will indicate the centre of gravity.
This method can be used to determine the centre of gravity of irregularly shaped objects since they are difficult to balance. You can also draw a third line in order to increase the accuracy of the experiment.
Stability:
Stability refers to the ability of an object to return to its original static equilibrium (or the original position) after it is displaced.
In order to understand stability, you should know some types of equilibrium.
- Stable equilibrium: When small externally induced displacements produce torques or forces that oppose the displacement allowing the body to return to its original equilibrium.
For instance, a brick lying on a level plain and a hanging pendulum (suspended freely).
In other words, the centre of gravity rises and returns to its original position as well.
- Neutral equilibrium: When externally produced small displacements do not produce any unbalanced forces (torques) that oppose the displacement allowing the body to remain in its new equilibrium.
In simple words, the centre of gravity remains at the same height. For instance, a football lying on a plane (level) surface.
- Unstable equilibrium: When the centre of gravity drops because the forces (torques) add to the displacement.
You should also know that the centre of gravity is dependent upon:
- Low centre of gravity
- Wider base area
This means that if the centre of gravity is kept as low as possible, the object will be more stable (the concept is applied to the racing cars).
Similarly, if the height is increased and the base area is kept wider, the stability also increases.
Conclusion:
With this, the topic of turning effect of forces has come to an end. I hope that all your queries have been addressed.
You should practise past paper questions from this topic because it is a very important topic from examination point of view. The topics covered in this article are listed below for your guidance.
- Moment of a force (torque)
- Principle of moments
- Centre of gravity
- Types of equilibrium
- Stability
Thank you very much for reading and staying with me till the end and stay tuned for more.


Comments
Post a Comment